分析电池的热行为和热关系效应的研究方法有很多。最常用的方法是实验法和数值模拟法。最常用的数值模拟方法是计算流体动力学(CFD)和有限元法(finite element method)。元法,FEM),电池热行为的数学模型或数值模型,一般由以下三部分组成:①能量守恒方程;②简化或复杂的电池发热方程;③ 边界条件方程,包括线性/非线性、热传导/对流热交换/辐射热交换等。目前很多电池热模型用于描述温度曲线或预测温度随时间的变化。Catherino 建立了一个热数学模型来研究铅酸电池的热失控行为。干等人。得到了二维和三维的圆柱形和方形锂离子电池,并得到了电池内部的温度分布。
研究电池热行为的数学模型很多,但主要有以下几种:
(1) 集中参数电池热模型;
(2) 简化的一维热学数学模型;
(3) 一维热电化学耦合模型;
(4) 圆柱电池二维瞬态传热模型;(5)锂离子电池
三维热滥用模型;(6) 二维锂离子电池CFD模型。
集总参数电池热模型最初由美国国家可再生能源实验室的Steve Burch提出,后由Johnson改进。模型散热量由公式(1)计算
Q d =(T b -T air )/R eff ——(1)
式中,R eff为有效热阻,即
R eff =(1-hA)-(t/kA)——(2)
其中h为表面传热系数,由电池温度决定,即h= h={
h forced =a[(m/ρA)/5] b , T b >T set
{ h性质=4,T b < T集——(3)
式(1)中电池周围的空气温度T air
为T air =T amb +[(0.5Q d )/m air c p·air ] ——(4)
Al-Hallaj 等人。使用简化的一维集中参数热数学模型来模拟圆柱形锂电池内部的温度分布(索尼,US18650)。数学模型中的能量方程为
(Ə²T/ər²)+(1/r)(əT/ər)+(q/k cell )=(1/α)(ƏT/Ət)——(5)
式中,kcell为电池的导热系数;α 是热扩散系数;q为热源,由电池产生的热量Q转化而来,即
Q=△G+T△S+W el ——(6)
Q=Q/V b ——(7)
其中 S 是熵。式(6)中G为吉布斯自由能,W el为电功,分别由式(8)和式(9)求得
△G=-nFE oc ——(8)
W el =-NFE—— (9)
式中,n为电子数;F是法拉第常数;E为电池电压;E oc是开路电压。电池的总热功率Q'可以表示为
Q'=I[(E oc -E)+T(dE oc /dT)]——(10)
A-Hallaj假设t=T a at t=t 0,即电池初始温度等于环境温度,Al-Hallaj设定的边界条件为
(dT/dr)| r=0 =0
-k细胞(dT/dr)| r=R =h(TT a ) ——(11)
一侧是绝热边界,另一侧是对流传热边界。
Forgez 等人。还使用一维热模型来预测 LiFePO 4 /石墨锂离子电池的热响应。使用的热源是
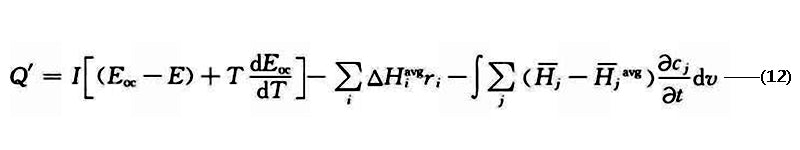
其中 ΔH 是焓变;r i是反应速率;c j为反应浓度;- H j是局部组分焓,- H j avg 是平均组分焓;下标 i 为化学反应类型;
Smith 和 Wang 使用复杂的一维集总参数热电化学耦合数学模型研究了电压为 276 V、容量为 6 A·h 的 HEV 锂离子电池组的脉动功率极限和热行为,该电池组由 72细胞。,该模型如图 1 所示。模型中使用的控制方程如下。
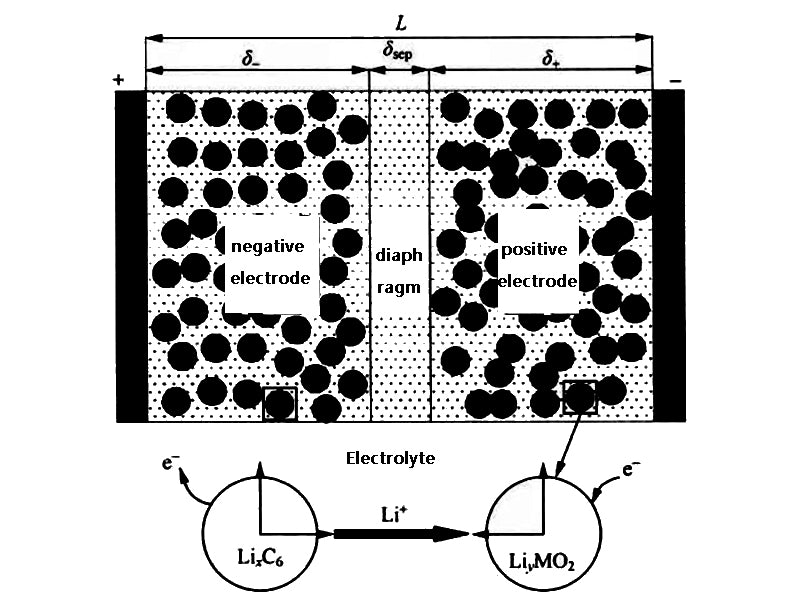
图1 锂离子电池模型
电解质
Əε e c e /ət=(ə/əx)[D eff e (ə/əx)c e ]+[(1-t 0 + )/F]J Li ——(13)
solid
Əc s /ət=(D s /r²)(ə/əx)[r²(əc s /ər)]——(14)
电解液(充电)
(Ə/Əx)[k eff (Ə/Əx)Ф e ]+(Ə/Əx)[k eff D (Ə/Əx)lnc e ]+J Li =0——(15)
固体(带电)
(Ə/Əx)[k eff (Ə/Əx)Ф s ]=J Li ——(16)
式中,ε为体积分数;c是锂离子的浓度;D为 式中,ε为体积分数;c是锂离子的浓度;D为锂离子的扩散系数;k是电解液的电导率;k D为扩散电导率;t 0 +为锂离子转移次数;J为电流密度;Ф为平均势能;下标e代表电解质;下标s代表实心。JLi可由式(17)得到
J Li =a s i o {exp[(α a F/RT)(η-(R SEI /a s )J Li )]-exp[(α c F/RT) (η-(R SEI /as )J李)]}—(17)
式中,io为单次反应产生的电流密度;a s为电极产生电流的有效面积;α a和α c分别为正极和负极的电化学反应转化系数;R是气体常数;R SEI为SEI电阻;η为单电极反应过电压由式(18)求得
η=Ф s -Ф e -E oc ——(18)
式中,Φ s和Φ e分别为电池的正负极电位。等式(8)至(11)中的其他参数由下式得到
D eff e =D e ε p e ——(19)
k eff =kε p e ——(20)
K eff D =(2RTk eff / F)(t 0 + -1){1+[dln(lnf±)]/dln(lnc e )]}——(21)
σ eff =ε s σ——(22)
σ s =3ε s /r秒=3(1-ε e -ε p -ε f )/r s ——(23)
吴等。使用圆柱电池的二维非稳态传热模型来模拟锂离子电池内部的温度分布。电池模型的径向导热系数k r不等于轴向导热系数k z,其能量方程同式(4) 反之,考虑导热系数的各向异性,则为
ρC p (əT/ ət)=k r (1/r)(ə/r)(rəT/ər)+k z (ə²T/əz²)+q——(24)
吴等。通过将数值模拟结果与实验进行对比,分析了自然对流冷却、强制对流冷却和热管冷却的效果。使用的边界条件如下:
{əT/ər=0,r=0,0<z<Z
{-k r (əT/əz)=h r (TT ∞ ), r=R, 0<z<Z
{k z (əT/əz)=h z (TT ∞ ), z=0, 0<r<R
{-k z (əT/əz)=h z (TT ∞ ), z=Z, 0<r< R——(25)
翅片边界条件为
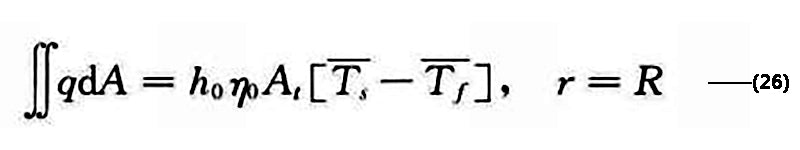
初始时刻 T=T ∞ , t=0, 0<r<R, 0<z<Z。图2为二维非稳态模型模拟的不同放电电流下电池温度随SOC的变化
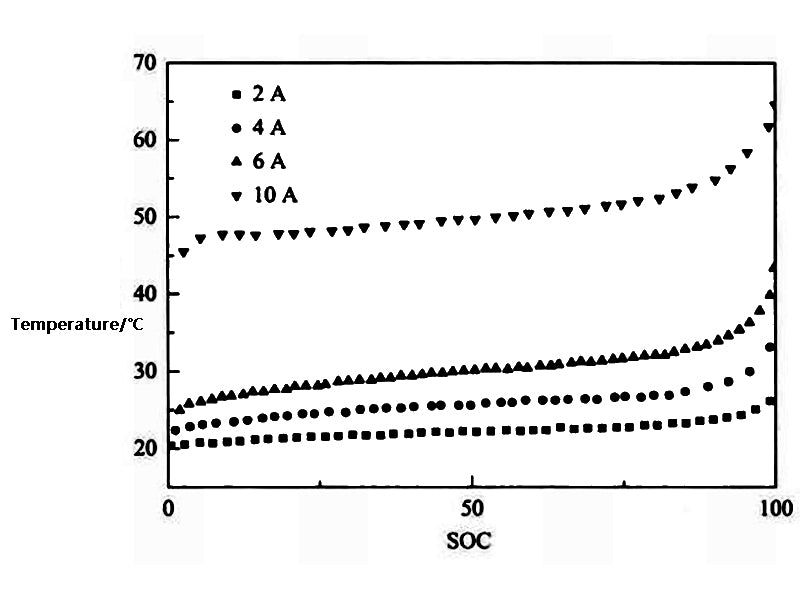
图2 不同放电电流下电池温度随SOC的变化
金等人。构建了锂离子电池热滥用的 3D 模型。模型的热源为
q=q abuse +q joul +q combustion +… -- (27)
式中,q joul和 q combustion分别表示焦耳热和反应热;q abuse为热滥用后的附加发热量,由式(27)计算
q abuse =q sei +q ne +q pe +q ele +q nb ——(28)
式中,q sei为SEI分解反应产生的热量;q ne为负极活性物质与电解液反应产生的热量;q pe为正极活性物质与电解液反应产生的热量;q ele为电解液分解反应产生的热量,q nb为正负极反应产生的热量,由下式计算
q i =H i W i R i ,i=sei ,ne,pe,ele,nb——(29)
R sei =A sei exp[-(Ea,sei )/RT]c m sei sei——(30)
R ne = A ne exp[-(t sei /t sei,ref )]c mpe.n neg exp[-(E a,ne )/RT ] -- (31)
R pe =A pe α m pe.pl (1-α) m pe.p2 exp[-(E a,pe )/RT] -- (32)
R ele =A ele exp[- (E a,ele )/RT]c m ele ele -- (33)
Kim 等人的模型。主要关注电池发热急剧增加情况下的热失控行为,特别是热化学反应机理。
李等。使用三维模型研究了运行和环境条件对电池组热行为的影响,并进一步研究了模型在 42V 电动汽车系统上的可靠性。表中显示了不同环境温度和循环时间下的最高和最低电池温度。1 所示。

表1 不同环境温度和循环次数下电池的最高温度和最低温度
金等人。建立容量为10A·h的方形锂聚合物电池的二维CFD模型,其中电流密度J由Newman和Tiedemann建立的公式(34)得到 J=Y(
V p -V n -U )——(34)
式中,Vp 、 Vn分别为电池正负极电位;Y和U为拟合得到的参数,拟合公式由Gu等人建立。
U=a0+a1(DOD)+a2(DOD)²+a3(DOD)³——(35)
Y=a4+a5(DOD)+a6(DOD)²——(36)
式中ai(i=0、1、2、3、4、5、6)为实验得到的常数,式(35)、式(36)中DOD(放电深度)为深度放电量,由式(2-37)求得。
DOD=∫ t 0 Jdt/Q T ——(37)
式中,QT red为单位面积的理论容量。
电池产生的热量为
Q=aJ[E oc -ET(dE oc /dT)]+a p r p i² p +a n r n i² n ——(38)
式中,a p和a n分别为正极和负极的比表面积;i p和 i n分别为正极和负极的电流密度;E oc为开路电压;E是电池电压:(dE oc /dT)是熵变。假设电池外部采用自然对流散热,则电池的散热率q conv
为q conv =2h/d(TT air )——(39)
结合方程(4)和(5),可以得到电池模型中的能量守恒方程
ρC p (əT/ət)=(ə/əx)[k x (əT/əx)]+(ə/əy)[ k y (əT/əy)]+qq conv ——(40)
根据Eq.建立的能量守恒方程。(40),金等人。模拟了方形电池在放电过程中的热行为,模型如图3所示。放电率低时仿真结果与实验结果的误差较小,放电率增大时误差逐渐增大。
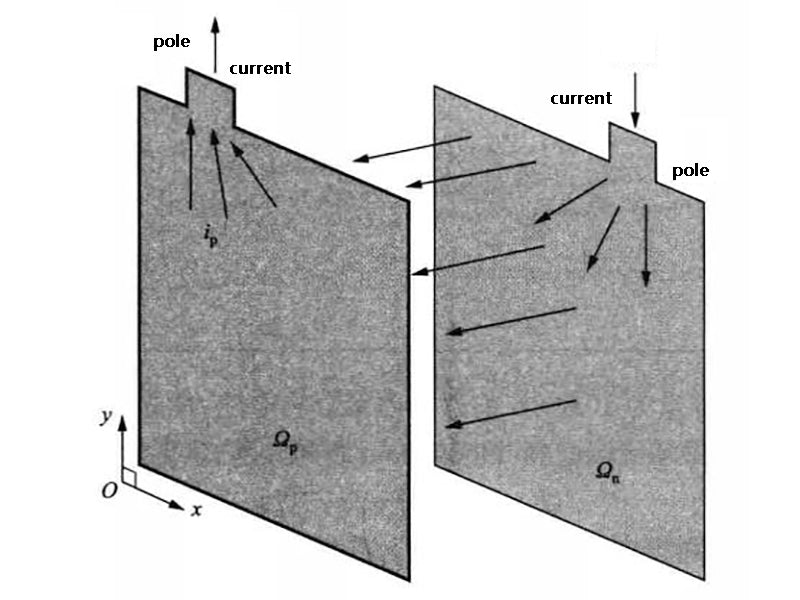
图3 二维电池产热模型示意图
上一篇我们送上的文章是
什么是风冷电池冷却的串联和并联通风? , _!在下一篇继续做详细介绍,如需了解更多,请持续关注。
本文由
日本NEC锂电池中国营销中心于2023-04-22 11:44:04 整理发布。
转载请注明出处.